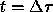 reach the bottom at
times
reach the bottom at
times 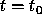 and
and 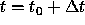 . Prove that, so long as
. Prove that, so long as  (i.e. the rocket moves non- relativistically), one has
(i.e. the rocket moves non- relativistically), one has
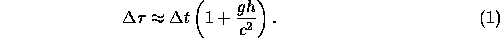
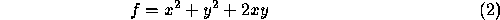
is a scalar and

are two vectors.
(2a) Compute f as a function of polar coordinates 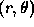 and
find the components of
and
find the components of 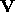 and
and 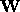 on the polar
basis, expressing them as functions of r and
on the polar
basis, expressing them as functions of r and 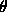 .
.
(2b) Find the components of 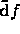 in Cartesians and obtain
them in polars by (i) direct calculation in polars, and (ii)
transforming from Cartesian coordinates.
in Cartesians and obtain
them in polars by (i) direct calculation in polars, and (ii)
transforming from Cartesian coordinates.
(2c) Use the metric tensor in polar coordinates to find the polar
components of the one- forms 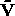 and
and 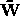 associated with
associated with 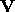 and
and 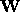 . Obtain these components by
transformation of the Cartesian coordinates of
. Obtain these components by
transformation of the Cartesian coordinates of 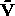 and
and
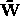 .
.
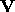 of question (2)
above, compute;
of question (2)
above, compute;
(3a) 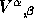 in Cartesian coordinates;
in Cartesian coordinates;
(3b) the transformation 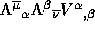 to polars;
to polars;
(3c) the components 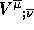 using the
Christoffel symbols given in the lecture notes [ Why is this the same as
(3b)?];
using the
Christoffel symbols given in the lecture notes [ Why is this the same as
(3b)?];
(3d) the divergence 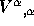 in Cartesian coordinates;
in Cartesian coordinates;
(3e) the divergence 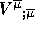 in polars
using part (3c);
in polars
using part (3c);
(3f) and the divergence 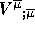 using
the formula given in the lecture notes.
using
the formula given in the lecture notes.
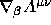 for all possible
indices in polar coordinates for the tensor with polar components
(
for all possible
indices in polar coordinates for the tensor with polar components
(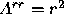 ,
,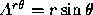 ,
, 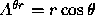 ,
,
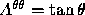 )
)